Закон Кулона. Электростатическое поле и его напряженность. Силовые линии. Принцип суперпозиции электростатических полей. Пример применения принципа суперпозиции при расчете напряженности: а) поля на оси тонкого равномерно заряженного кольца; б) поля равномерно заряженной прямой нити конечной длины; в) поля на оси тонкого равномерно заряженного диска.

Закон Кулона: Сила взаимодействия двух точечных зарядов направлена вдоль прямой линии, соединяющей заряды, прямо пропорциональна произведению обоих зарядов и обратно пропорциональна квадрату расстояния между ними.

Закон Кулона:  , где r – расстояние между зарядами, k – коэффициент пропорциональности (k=9*109 [Н*м2/Кл2]) (q – [Кл], ε – [Ф/м])

Закон Кулона (в векторной форме):  (F12 и r12 – вектора)

Заряд, равный одному кулону, определяют как заряд, проходящий за одну секунду через поперечное сечение проводника, по которому течет постоянный ток силы один ампер.

Электростатическое поле: Поле, создаваемое неподвижными зарядами.

Напряженность электростатического поля: E=F/q₀ (напряженность и сила – вектора)

Силовые линии: Линии, касательные к которым в каждой точке совпадают с направление вектора Е.

Принцип суперпозиции электростатических полей: Напряженность Е_Σ результирующего поля, создаваемая системой зарядов, равна геометрической (векторной) сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Поток вектора напряженности электростатического поля. Формулировка и доказательство теоремы Остроградского-Гаусса для напряженности электростатического поля в вакууме в интегральной форме. Применение теоремы Остроградского-Гаусса для расчета напряженности поля: а) равномерно заряженной бесконечной плоскости; б) двух параллельных бесконечных плоскостей, заряженных равномерно разноименными зарядами с поверхностными плоскостями σ и -σ; в) равномерно заряженного по объему шара; г) равномерно заряженного по объему бесконечного цилиндра.

Вывод и формулировка теоремы Остроградского-Гаусса для вектора напряженности электростатического поля в дифференциальной форме. Источники и стоки поля.

Формулировка и доказательство теоремы о циркуляции вектора Е.

Потенциал электростатического поля. Принцип суперпозиции для потенциалов. Вывод связи между потенциалом электростатического поля и его напряженностью. Эквипотенциальные поверхности.

Электрический диполь. Поле электрического диполя. Сила, действующая на диполь во внешнем электростатическом поле.

Электрический диполь - система из двух одинаковых по модули и разноименных зарядов.

Поле электрического диполя - сам диполь точечный, т.е. расстояние r от диполя до точки наблюдения >> L.

Сила, действующая на диполь во внешнем электростатическом поле:

При перемещении дипольных молекул в электрическое поле на каждую молкулу будут действовать силы поля, стремящиеся установить ее по направлению линий поля.

Вещество в электростатическом поле. Микро- и макро-поле. Проводники в электростатическом поле. Поле внутри и снаружи проводника. Поле у поверхности проводника.

Общая задача электростатики. Уравнение Пуассона. Уравнение Лапласа. Метод изображений.

Электроемкость. Электроемкость уединенного проводника. Конденсаторы. Вывод емкости: а) плоского конденсатора; б) сферического конденсатора; в) цилиндрического конденсатора.

Вещество в электростатическом поле. Микро- и макро-поле. Диэлектрики. Электрическое поле в диэлектрике. Поляризация. Связанные и сторонние заряды.

Поляризованность диэлектрика. Связь между поляризованностью Р и напряженностью Е. Формулировка и доказательство теоремы Отсроградского-Гаусса для поля вектора поляризованности Р в интегральной и дифференциальной формах. Граничные условия для вектора поляризованности Р.

Электрическая индукция D. Формулировка и доказательство теоремы Остроградского-Гаусса для поля вектора D в интегральной и дифференциальной формах. Связь между векторами D и E. Условия для векторов E и D на границе раздела двух диэлектриков.

Энергия электростатического поля. Энергетический подход к взаимодействию. Энергия взаимодействия системы точечных зарядов. Полная энергия электрического взаимодействия. Энергия заряженных проводника и конденсатора. Плотность энергии электрического поля.

Электрический ток. Плотность тока. Связь плотности тока со скоростью упорядоченного движения зарядов в проводнике. Связь между силой тока и вектором плотности тока.

Электродвижущая сила. Сторонние силы и их природа. Связь между ЭДС и вектором напряженности сторонних сил. Напряжение.

Закон Ома для однородного участка цепи. Закон Ома в дифференциальной форме. Закон Ома для замкнутой цепи. Закон Ома для неоднородного участка цепи.

Однородный участок цепи - участок не содержащий источников ЭДС.

Закон Ома: I=U/R

Закон Ома в дифференциальной форме: I=(U*S)/(L*ρ)

R=ρ*L / S

U=E*L

j=I/S

γ=1/ρ

=> I/S = E * 1/ρ

j=γ*E

Закон Ома для замкнутой цепи: I=ε/(R+r)

Закон Ома для неоднородного участка цепи: I=(φ1-φ2)/R

Работа и мощность тока. Закон Джоуля-Ленца. Удельная тепловая мощность тока. Вывод закона Джоуля-Ленца в дифференциальной форме.

Если участку цепи постоянного тока приложить напряжение U, то за время Δt через сечение проводника переносится заряд dq.

dq=I*dt

Работа тока: dA=U*dq=U*I*dt

Мощность тока: P=dA/dt=U*I=(φ₁-φ₂)*I+ε₁₂*I

Мощность тока выделяется во внешней цепи: P=U*I=I²*R=U²/R

Закон Джоуля-Ленца: Если электрический ток течет по неподвижному металлическому проводнику, то работа тока идет на нагревание проводника.

Закон Джоуля-Ленца: dQ=dA=I*U*dt=I²*R*dt=U²*dt/R

Удельная тепловая мощость тока: W=dQ/(dV*dt)

Вывод закона Джоуля-Ленца в дифференциальной форме:

Выделим в проводнике элементарный цилиндр, ось которого совпадает с направлением тока.

dV=dS*dL

R=ρ*dL/dS

По закону Джоуля-Ленца за время dt в этом цилиндре выделится количество теплоты: dQ=I²*R*dt=(j*dS)²*(ρ*dL/dS)*dt=j²*dS*dL*ρ*dt=j²*ρ*dV*dt

dQ/(dV*dt)=W=j²*ρ

Вспомним закон Ома в дифференциальной форме: j=γ*E=E*(1/ρ)

Получаем закон Джоуля-Ленца в дифференциальной форме: W=j²*ρ=(1/γ)*j²=(1/γ)*γ²*E²=γ*E²=j*E

Правило Кирхгофа.

Узел электрической цепи - любая точка цепи в которой сходится не менее трех проводников с током. Ток, входящий в узел, считается положительным, а ток выходящий из узла - отрицательный.

Первое правило Кирхгофа: Алгебраическая сумма токов, схлдящихся в узле равна 0.

Второе правило Кирхгофа: В любом замкнутом контуре произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивление Ri соответсвующих участков этого контура, равна алгебраической сумме ЭДС (алгебраическая сумма ЭДС = алгебраической сумме падений напряжения).

Магнитное поле, его проявление и обнаружение. Магнитный момент рамки с током. Вращающий момент сил, действующий на рамку с током в магнитном поле. Магнитная индукция В. Силовые линии магнитного поля.

Подобно тому, как в пространстве окружабщему электрические заряды возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты возникает силовое поле, называемое магнитным полем.

Наличае магнитного поля обнаруживается по силовому действию на внесенные в проводники с током постоянные магниты.

Название "магнитное поле" связывают с ориентацией магнитных стрелок под действием поля создаваемого током, это явление впревые обнаружено датским физиком Эрстетом.

Важнейшие особенности магнитного поля в том, что оно действует только на движующиеся в нем электрические заряды.

Магнитный момент рамки с током: P_m=I*S*n (P и n - вектора)

Вращающий момент сил: M=[P_m B] (все вектора)

Вращающий момент сил (максимальный): M_max=P_m* B*

Магнитная индукция определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным 1.

Линии магнитной индукции - это линии, касательные к которым в каждой точке совпадают с направлением вектора B.

Линии магнитной индукции всегда замкнуты и охватывают проводники с током.

Поля макро- и микро-токов. Гипотеза Ампера. Вектор напряженности магнитного поля Н. Связь между величинами В и Н.

В любом поле существует микроскопическое поле, обусловленное движением электронов в атомах и молекулах. Эти микроскопические токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротока.

Например, если вблизи каково-то тела поместить проводник с током, то под действием его микротока ориентируются определенным образом.

Вектор В характеризует результирующее магнитное поле, создаваемое макро- и микро-током. т.е. в одном и том же токе и при прочих равных условиях вектор В в различных средах имеет разное значение.

Гипотеза Ампера: в каждом веществе за счёт движения электронов возникают микротоки.

Вектор Н - напряженность магнитного поля, характеризует поле макротоков.

Связь между величинами В и Н: B=μ₀*μ*H

μ₀ - магнитная постоянная

μ - безразмерная постоянная, магнитная проницаемость среды

Закон Био-Савара-Лапласа. Принцип суперпозиции магнитных полей и его применение для расчета магнитного поля: а) прямого тока; б) на оси кругового тока.

(r³)

Закон Ампера.

Направление силы F, с которой магнитное поле действует на прямолинейный проводник с током I, всегда перпендикулярно к проводнику и к направлению магнитной индукции В. На проводники, расположенные вдоль направления линий магнитного поля, поле не действует.

Если расположить левую ладонь так, чтобы вытянутые пальцы указывали направление тока, а линии магнитного поля впивались в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник.

Закон Ампера: F=B*I*L*sinφ , где B – магнитная индукция, I – сила тока, L – длина прямолинейного проводника с током, φ – угол между вектором В и проводником с током I.

dF_A=I*[dL B] (все кроме тока - вектора)

Когда проводник параллелен индукции В (φ=0), то F=0.

Действие магнитного поля на движущийся заряд. Сила Лоренца. Эффект Холла.

Теорема о циркуляции вектора В и ее применение для определения магнитного поля: а) соленоида; б) тороида; в) внутри и снаружи прямого проводника с током.

Работа по перемещению проводника и контура с током в магнитном поле.

Явление электромагнитной индукции. ЭДС электромагнитной индукции. Закон Фарадея. Правило Ленца. Связь закона Фарадея и правила Ленца с законом сохранения энергии.

Явление электромагнитной индукции — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

ЭДС электромагнитной индукции:

Фв — магнитный поток через поверхность, натянутую на этот контур.

Закон Фарадея:

N - число витков

Фв - магнитный поток через один виток

Закон Фарадея в дифференциальной форме:

Правило Ленца: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток.

Связь закона Фарадея и правила Ленца с законом сохранения энергии:

Закон Фарадея (см. (2)) может быть выведен из закона сохранения энергии , как это впервые сделал Г. Гельмгольц. Возьмем проводник с током I, помещенный в однородное магнитное поле, которое перпендикулярное плоскости контура, и может свободно двигаться (см. рис. 1). Под действием силы Ампера F, направление которой показано на рисунке, проводник передвигается на отрезок dx. Значит, сила Ампера производит работу dA=IdФ, где dФ — пересеченный проводником магнитный поток.

Используя закон сохранения энергии , работа источника тока за время dt ( ξIdt ) будет складываться из работы на теплоту Джоуля-Ленца (I2Rdt) и работы по перемещению проводника в магнитном поле (IdФ):

, где R — полное сопротивление контура.

Значит:

-(dФ/dt) = ξi есть как раз закон Фарадея (2).

Индуктивность контура. Самоиндукция. ЭДС самоиндукции.

Индуктивность контура - физическая величина определяющая магнитные свойства цупи.

Ф_B=L*I (Ф_B - поток через контур, L - индуктивность)

Индуктивность - поток сцепленный с контуром приходящийся на единичный ток.

Единица индуктивности: 1 [Гн] (Генри)

Самоиндукция - ЭДС возникающая в проводящем контуре при изменении в нем силы тока.

ЭДС самоиндукции:

Взаимная индукция. Трансформаторы.

Взаимная индукция - величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура, то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром

Трансформатор - электрическая машина, имеющая две или более индуктивно связанные обмотки и предназначенная для преобразования посредством электромагнитной индукции одной или нескольких систем переменного тока в одну или несколько других систем переменного тока.

Энергия магнитного поля. Энергия магнитного поля, связанная с контуром. Энергия магнитного поля соленоида. Объемная плотность энергии магнитного поля.

Магнитные свойства вещества. Диа- и парамагнетики.

Магнитные свойства вещества:

Антиферромагнетики — магнитные моменты вещества направлены противоположно и равны по силе.

Диамагнетики — вещества, намагничивающиеся против направления внешнего магнитного поля.

Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля.

Ферромагнетики — вещества, в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов

Ферримагнетики — материалы, у которых магнитные моменты вещества направлены противоположно, но не равны по силе.

Диа- и парамагнетики:

Намагниченность J. Связь между векторами J и H. Вектор магнитной индукции В, как результирующего поля в веществе. Связь между векторами В, Н и J.

Намагниченность J - магнитный момент единицы объема магнетика.

J=P_m/V=ΣP_o/V (все вектора, кроме V, естественно)

P_m - магнитный момент магнетика в магнитном поле

P_o - магнитный момент молекулы в магнитном поле

Связь между векторами J и H: J=χ*H (χ - хи, магнитная восприимчивость)

Вектор магнитной индукции В, как результирующего поля в веществе: B=B_o+B' (все вектора)

B_o - вектор магнитной индукции внешнего поля

B_o=μ_o*H

B' - вектор магнитной индукции поля намагниченного вещества

B'=μ_o*J

Связь между векторами В, Н и J:

B=B_o+B' , где B_o=μ_o*H и B'=μ_o*J (J=χ*H) , следовательно B=μ_o*(1+χ)*H

μ=(1+χ) - магнитная проницаемость вещества

Теорема о циркуляции вектора Н.

Циркуляция вектора Н равна сумме макротоков.

Теорема о циркуляции вектора J.

Циркуляция вектора намагниченности равна сумме охваченных микротоков.

Условия на границе раздела двух магнетиков. Нормальные составляющие векторов В и Н на границе раздела. Тангенсальные составляющие векторов В и Н на границе раздела.

Условия на границе раздела двух магнетиков:

В соответсвии с теоремой Гаусса имеем: B_n2*ΔS - B_n1*ΔS = 0

B_n1=B_n2

Нормальные составляющие векторов В и Н на границе раздела:

B_n1=μ₀μ₁H_n1

B_n2=μ₀μ₂H --------------> H_n1/H_n2=μ₂/μ₁

Тангенсальные составляющие векторов В и Н на границе раздела:

=0 (по теореме о циркуляции)

H_τ2L-H_τ1L=0

H_τ2=H_τ1

H_τ1=B_τ1/(μ₀μ₁)

H_τ2=B_τ2/(μ₀μ₂) -------------> B_τ2/B_τ1=μ₁/μ₂

Ферромагнетики и их свойства. Петля магнитного гистерезиса. Магнитотвердые и магнитомягкие ферромагнетики. Природа магнитного гистерезиса. Области спонтанной намагниченности. Перемагничивание ферромагнетика путем смещения доменной стенки. Скачки Баркгаузена.

Ферромагнетики - вещества, характеризуются наличаем областей спонтанной намагниченности.

Свойства ферромагнетиков:

- Ферромагнетики сильно втягиваются в область более сильного магнитного поля.
- Магнитная восприимчивость ферромагнетиков положительна и значительно больше единицы.
- При не слишком высоких температурах ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий.

Петля магнитного гистерезиса.

Br - остаточная намагниченность

Нс - коэрцитивная сила

Магнитотвердые ферромагнетики - магнитные материалы, характеризующиеся высокими значениями коэрцитивной силы Hc.

Магнитомягкие ферромагентики - материалы с малой коэрцитивной силой и высокой магнитной проницаемостью. Они обладают способностью намагничиваться до насыщения в слабых магнитных полях, характеризуются узкой петлей гистерезиса и малыми потерями на перемагничивание.

Природа магнитного гистерезиса:

Выделяют три основные причины возникновения магнитного гистерезиса:
• магнитный гистерезис, связанный с необратимым смещением доменных границ;
• магнитный гистерезис, связанный с необратимым вращением спонтанной намагниченности;
• магнитный гистерезис, связанный с задержкой образования и роста зародышей перемагничивания.

Домены — области однородной спонтанной намагниченности, у которых величина намагниченности (магнитного момента единицы объема) одинакова, а направления различны.

Перемагничивание ферромагнетика путем смещения доменной стенки.

При помещении ферромагнетика в магнитное поле направление намагниченности в нем может изменяться и в кбнце концов способно стать одинаковым для всего ферромагнетика . Изменение направления намагниченности называется перемагничиванием . До самого последнего времени исследовались в основном лишь равновесная или квазиршвновесная доменная структуры ферромагнетика , наблюдаемые в постоянных или медленно меняющихся магнитных полях. При медленных изменениях магнитного поля процесс перемагничивания ферромагнетика происходит путем либо смещения границ между доменами, так называемых доменных стенок , либо поворота намагниченности внутри домена.

Очень часто процесс перемагничивания необходимо убыстрить. Это относится, например, к устройствам памяти электронных вычислительных машин. От скорости перемагничивания зависит быстродействие машины.

Скачки Баркгаузена - скачкообразное изменение намагниченности ферромагнитных веществ при непрерывном изменении внешних условий, например магнитного поля.

Электромагнитные волны. Феноменологические уравнения Максвелла. Волновые уравнения для векторов Е и Н.

Электромагнитные волны - возмущение электромагнитного поля, т.е. переменного во времени и пространстве электромагнитное поле, распростроняющееся в пространстве.

Феноменологические уравнения Максвелла:

Ротор - векторное произведение оператора Набла на вектор.

Волновые уравнения для векторов Е и Н: (???)

Энергия электромагнитных волн. Модуль плотности потока энергии. Вектор Умова-Пойнтинга.

Электромагнитные волны переносят энергию в соответствии с формулой (бегущая волна) имеет формулу для плотности потока энергии: j=W*v, где j - плотность потока энергии.

Плотность энергии электромагнитной волны представляет собой сумму плотности энергии электрического и магнитных полей: W=W_E+W_H.

W_E=(ε₀*E²)/2

W_H=(μ₀*H²)/2

Модуль плотности потока энергии: П=W*c=E*H

Вектор Умова-Пойнтинга: П=[E H] (все вектора)

Теорема Пойнтинга.

Убыль энергии в данном объеме в единицу времени равна потоку энергии сквозь поверхность этого объема + мощность развиваемая полем при совершении работы над зарядами вещества внутри данного объема.

Импульс элетромагнитного поля.

Электромагнитная волна поглащается в каком-либо теле или отражается от него, т.е. взаимодействует с телом, оказывает на это тело давление и придает телу импульс.

Импульс электромагнитного поля, динамическая характеристика поля — количество движения, которым обладает электромагнитное поле в данном объёме. Тела, помещенные в электромагнитное поле, испытывают действие механических сил. Воздействие поля на тело при этом связано с поглощением телом электромагнитных волн или изменением направления их распространения (отражение, рассеяние, преломление). При излучении телом электромагнитных волн, в частности света, импульс тела также меняется. Так как импульс замкнутой материальной системы в результате излучения, поглощения или отражения электромагнитных волн не может измениться (в силу закона сохранения полного импульса системы), то из этого следует, что электромагнитная волна также обладает импульсом.

Взаимодействие электромагнитных волн с веществом. Электронная теория дисперсии. Нормальная и аномальная дисперсия. Закон Бугера. Рассеяние света.

Взаимодействие электромагнитных волн с веществом: В линейном приближении взаимодействие электромагнитных волн с веществом описывается небольшим числом параметров. Например, однородный и изотропный диэлектрик описывается одной величиной либо диэлектрической восприимчивостью , либо диэлектрической проницаемостью εr, которые являются функциями частоты. Скорость распространения и длина волны , распространяющейся в диэлектрике, зависят от диэлектрической проницаемости вещества εr, т. е. в веществе наблюдается дисперсия электромагнитных волн (дисперсией называется зависимость фазовой скорости распространения волны от ее частоты). От дисперсии зависит то, как распространяются электромагнитные волны разных частот в различных веществах .

Электронная теория дисперсии:

Классическая электронная теория дисперсии рассматривает дисперсию света как результат вынужденных колебаний электронов, входящих в состав атома, под действием поля электромагнитной волны.

Нормальная дисперсия — вид дисперсии света, при которой показатель преломления среды увеличивается с увеличением частоты световых колебаний.

Аномальная дисперсия — вид дисперсии света, при которой показатель преломления среды уменьшается с увеличением частоты световых колебаний.

Закон Бугера — Ламберта — Бера — физический закон, определяющий ослабление параллельного монохроматического пучка света при распространении его в поглощающей среде.

Закон выражается следующей формулой:

,

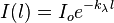где I0 — интенсивность входящего пучка, l — толщина слоя вещества, через которое проходит свет, kλ — показатель поглощения (часто неправильноименуется коэффициентом поглощения).

Показатель поглощения характеризует свойства вещества и зависит от длины волны λ поглощаемого света. Эта зависимость называется спектром поглощения вещества.

Рассеяние света, изменение характеристик потока оптического излучения (света) при его взаимодействии с веществом. Этими характеристиками могут быть пространственное распределение интенсивности, частотный спектр, поляризация света. Часто рассеяние света называется только обусловленное пространственной неоднородностью среды изменение направления распространения света, воспринимаемое как несобственное свечение среды.

Отражение и преломление световых волн.

Если световая волна распространяется в однородной среде без препятствий, то волна распространяется по прямым линиям — лучам. На границе раздела двух однородных сред лучи отражаются  и  преломляются (рис.1). Отраженный (3)  и  преломленный (2) лучи находятся в одной плоскости с падающим лучом (1)  и  перпендикуляром к границе раздела двух сред (). Угол падения равен углу  отражения  . Угол  преломления  можно найти из равенства

,

где  и   — показатели  преломления  первой  и  второй среды.

Интерференция света. Когерентность пространственная и временная. Методы получения когерентных источников света. Расчет интерференционной картинки с двумя источниками.

Интерференция света - частный случай интерференции волн заключающихся в пространственном перераспределении энергосветового излучения при суперпозиции электромагнитных волн.

Пространственная когерентность - когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках поверхности перпендикулярной направлению распространения волны.

Временная когерентность - когерентность колебаний, которые совершаются в одной и той же точке пространства и определяемая степенью монороматичности волн.

Методы получения когерентных источников света: Когерентные источники получают, разделив световую волну, идущую от одного источника на две (опыт Юнга, зеркала Френеля).

Расчет интерференционной картинки с двумя источниками.

Интерференция света в тонких пленках.

Интерференция света — нелинейное сложение интенсивностей двух или нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности.

Интеpфеpенцию в тонких пленках можно наблюдать двумя способами. Один способ основан на том, что пленка имеет pазличную толщину в pазных местах, дpугой - на том, что свет может падать на пленку под pазными углами. Пеpвый способ дает так называемые полосы pавной толщины, втоpой - полосы pавного наклона.

Дифракция света. Принцип Гюйгенса и Гюйгенса-Френеля. Зоны Френеля. Расчет радиуса зон Френеля. Дифракция на круглом отверстии. Дифракция на круглом диске, пятно Пуассона. Дифракция Френеля и дифракция Фраунгофера.

Дифракция света - явление огибания светом преграды или прохождения через узкое отверстие.

Принцип Гюйгенса: Каждая точка, до которой доходит волновое возбуждение, является в свою очередь центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.

Принцип Гюйгенса-Френеля: Световая волна возбуждаемая источником света может быть представлена, как результат суперпозиции когерентных вторичных волн, излучаемым фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности охватывающей источник. Обычно в качестве такой поверхности выбирают одн из волновых поверхностей. В этом случае все фиктивные источники действуют синфазно. Таким образом для определения некоторой точки в пространстве результирующей интенсивности, нужно учесть интерференцию всех этих вторичных волн.

Френель исключил возможность возникновения обратных вторичных волн, предположил, что если между источником и точкой наблюдения находится прозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии такая же как при отсутствии экрана.

Зоны Френеля: Френель предложил разбить волновую поверхность на кольцевые зоны такого размера, чтобы расстояние от краев до точки наблюдения отличалось на λ/2. Колебания от соседних зон проходит до точки наблюдения расстояние отличающееся на λ/2 и приходит к точке наблюдения в противоположной фазе по отношению к предыдущему колебанию и при наложении эти колебания будут ослаблять друг друга.

Расчет радиуса зон Френеля:

(внешний радиус зоны Френеля под номером m)

Дифракция на круглом отверстии:Вид дифракционной картины зависит от числа зон Френеля укладывющихся на открытой части волновой поверхности.

Дифракция на круглом диске: Закрытые диском участки волнового фронта нужно исключить из рассмотрения, и зоны Френеля строить начиная с краев диска. Если диск закрывает m зон Френеля, то амплитуда результирующего колебания: A=A_m+1/2

Пятно Пуассона - светлое пятно, яркость которого с увеличением размера диска уменьшается.

Дифракция Френеля относится к случаю, когда на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся на конечном расстоянии от предмета.

Дифракция Фраунгофера (дифракция в параллельных лучах)относится к случаю, когда источник света и точка наблюдения бесконечно удалены от препятствия вызвавшего дифракцию.

Многолучевая интерференция. Дифракционная решетка. Дифракция рентгеновских лучей. Формула Вульфа-Бреггов.

Многолучевая интерференция:Интерференция, возникающая вследствие множественных отражений светового пучка при его распространении вдоль оптического пути системы.

Дифракционная решетка- система параллельных щелей и интервалов равной толщины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта.

Формула Вульфа-Бреггов: 2*d*sinθ = m*λ

Голография. Запись и воспроизведение голограмм. Применение голографии.

Голография — способ получения объемных изображений предметов на фотопластинке (голограмме) при помощи когерентного излучения лазера.

Запись информации и ее считывание осуществляются с помощью лазера.

Для воспроизведения объемного изображения голограмма помещается под излучение лазера той же длины волны, которая использовалась при записи голограммы. Зеркальный экран освещается потоком опорного света лазера и отраженного от голограммы. Происходит сложение этих волн, обратное тому сложению, которое производилось при записи голограммы, и на экране возникает объемное изображение объекта.

Основные особенности голографии, отличающие ее от фотографии, таковы: 1) это запись интерференционной картины, содержащая не только амплитудную, но и фазовую информацию, тогда как обычная фотография - это запись только интенсивностей света, не содержащая фазовой информации; 2) при регистрации голограммы нет необходимости в фокусировке, голограмма чаще всего не имеет сходства с объектом; 3) голограмма способна восстанавливать точную копию волнового фронта, идущего от объекта (если объект трехмерный, она восстанавливает трехмерное изображение); 4) изменяя угол между опорным пучком и волновым фронтом, идущим от объекта, можно на одном участке фотографической пластинки записать более одной голограммы; 5) в большинстве случаев для восстановления изображения достаточно любой малой части голограммы; если голограмма повреждена или частично уничтожена, она все равно восстановит изображение.

Поляризация света. Естественный и поляризованный свет. Закон Малюса. Закон Брюстера. Распространение электромагнитных волн в одноосных кристаллах. Двойное лучепреломление. Поляризационные призмы и поляроиды.

Поляризованный свет - свет в котором колебания светового вектора, каким то образом упорядочены.

Естественный свет - свет в котором все направления колебания светового вектора Е равновероятны.

Закон Малюса: I=I₀*cos²α

Закон Брюстера: Закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера.

Закон Брюстера: , где n21 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера).

Распространение электромагнитных волн в одноосных кристаллах:

Оптическая ось кристалла - направление в оптически анизотропном кристалле по которому распространяется луч света не испытывая двойного лучепреломления.

Одноосные и двухосные кристаллы - кристаллы с одним или двумя направлениями вдоль которых существует двойное лучепрломление.

Двойное лучепреломление — эффект расщепления в анизотропных средах луча света на две составляющие. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным, второй же отклоняется в сторону, нарушая обычный закон преломления света, и называется необыкновенным.

Поляризационные призмы, один из классов призм оптических. Поляризационные призмы служат линейными поляризаторами — с их помощью получают линейно поляризованное оптическое излучение. Обычно поляризационные призмы состоят из 2 или более трёхгранных призм, по меньшей мере одна из которых вырезается из оптически анизотропного кристалла.

Поляроид, поляризационный светофильтр, один из основных типов оптических линейных поляризаторов; представляет собой тонкую поляризационную плёнку, заклеенную для защиты от механических повреждений и действия влаги между двумя прозрачными пластинками (плёнками).

Тепловое излучение. Законы Кирхгофа, Вина и Стефана-Больцмана. Формула Рэлея-Джинса.

Тепловое излучение равновесно. Если нагретые тела поместить в полость ограниченную идельно отражающей оболочкой, то через некоторое время наступит равновесие, т.е. каждое тело будет в единицу времени излучать столько же энергии сколько и поглащать.

Закон Кирхгофа: Отношение спектральной плотности энергетической светимости, к спектральной поглащательной способности не зависит от природы тела. Оно является для всех тел универсальной функцией частоты и темпратуры.

Закон Кирхгофа (универсальная функция Кирхгофа; спектральная плотность энергетической светимости черного тела):

Черное тело - тело, способное плоностью поглащать, при любой температуре, все падающие на него излучения, любой частоты.

Закон (смещения) Вина: λ_max=b/T (b=2,9*10^-3 м*К)

Закон Вина: Длина волны λ_max ,соответствующая максимуму спектральной плотности энергетической светимости черного тела, обратно пропорциональна его термодинамической температуре.

Закон Стефана-Больцмана: R_e=σ*T⁴

Закон Стефана-Больцмана: Энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры.

Формула Рэлея-Джинса:

Гипотеза Планка. Формула Планка для теплового излучения. Корпускулярно-волновой дуализм. Фотоны.

Гипотеза Планка: Излучнение и погашение света происходит не непрерывно, а дискретно, т.е. определенными порциями (квантами).

ε=h*ню

h - постоянная Планка (h=6,63*10³⁴)

Формула Планка для теплового излучения:

Корпускулярно-волновой дуализм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.

Фотоны — кванты электромагнитного излучения, движутся со скоростью света и не существуют в состоянии покоя.

Законы внешнего фотоэффекта. Квантовая теория фотоэффекта.

Внешний фотоэффект - испускание электрона веществом под действием электромагнитного изменения.

Первый закон (закон Столетова): При фиксированной частоте падающего света, число фотоэлектронов вырываемых из катода за единицу времени пропорционально интенсивности света.

Второй закон: Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектрона не зависит от интенсивности падающего света, а а определяется только его частотой.

Третий закон: Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света ниже которой фотоэффект не возможен.

Квантовая гипотеза Планка: h*ню = ε

Формула Энштейна: h*ню = Авых + (m*v²)/2

Авых - работы выхода

Чем больше ню, тем больше кинетическая энергия.

Эффект Комптона и его объяснение.

Эффект Комптона: Упругое рассеивание коротковолнового высокочастотного электромагнитного излучения, (рентгеновского или гамма излучения) на свободных или связанных электронах вещества, сопротивляющегося увеличению длины волны.

Комптоновский сдвиг: Δλ = λ’-λ = 2*λ_c*sin²( θ/2 ) = λ_c*(1-cosθ)

λ_c = h/mc = 2,43 пм = 2,43 * 10-12 м

Эффект Комптона рассматривается, как упругое рассеивание фотона на свободном покоящемся электроне. Фотон упруго столкнувшись с электроном, передает ему часть своей энергии и импульса, и рассеивается. Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения.